目次
Contents
グラフと聞いて何を思い浮かべますか?
1. 円グラフ
2. 棒グラフ
3. 折れ線グラフ
一般的にぱっと思い浮かぶのは上記でしょうか。実はグラフには文脈によって分けるべき概念がいくつかあり、上記は統計グラフの種類のひとつずつでしかありません。統計グラフ以外にもグラフ理論、関数グラフなど様々なグラフがありますが、それは別の機会にして、今回は統計グラフおよび代表的なパラドックスについて説明を試みようと思います。
統計グラフ
総務省統計局の「なるほど統計学園」(※1)でどう説明しているか見てみましょう。
• グラフ
o数量を、見やすく図にしたもの。
なるほどシンプルですね。つぎに初級編のグラフの種類を見てみましょう。
1. 絵グラフ: 同形の絵を並べ、量の大小を比較する。
2. 棒グラフ: 棒の高さで、量の大小を比較する。
3. 折れ線グラフ: 量が増えているか減っているか、変化の方向をみる。
4. 円グラフ: 全体の中での構成比をみる。
5. 帯グラフ: 構成比を比較する。
6. ヒストグラム: データの散らばり具合をみる。
7. 箱ひげ図: データの散らばり具合をみる。
代表的なグラフが7つ並んでいます。それぞれの細かい解説は統計局に譲るとして、代表的なものだけで7つあります。ちゃんと目的ごとにどのグラフを使えばいいのか解説もされています。ヒストグラムと箱ひげ図はいずれも「データの散らばり具合を見る。」となっていますが、併用される場合が多いです。実は上記以外にも様々な統計グラフがあり、各種行政機関でも使用されています。それらを把握するために次に上級編のグラフの種類を見てみましょう。
1. パレート図: 全体に対する各項目の構成比の集中度合いをみる。
2. ローレンツ曲線: 集中の度合いをみる。
3. レーダーチャート: 複数の指標をまとめてみる。
4. 散布図: 2種類のデータの相関をみる。
5. バブルチャート: 2つの変量の相関関係に加えて円の面積で3つ目の変量をみる。(※2)
6. 統計地図: 地域別の比較をする。
見慣れないグラフが出てきましたね。文字数の関係もあり、ここも解説は統計局に譲りますが、初級編、上級編合わせて13種類もグラフがあります。
シンプソンのパラドックス
こういった統計グラフを読み解くうえでよく出てくるのがシンプソンのパラドックスです。
シンプソンのパラドックス(Simpson’s paradox)とは、統計学者のEdward H. Simpson(エドワード・シンプソン)氏が1951年に発表した論文で最初に提示されたもので、層別のグループデータにおいて、グループ別に見られる相関関係(前提)がグループを合計した全体でも成り立つだろうと直感的に推測されるのに対して、実際のデータ全体に見られる相関関係(結果)は、前提とは真逆になってしまう(あるいは一致しない)というパラドックス(逆説)現象を指します。
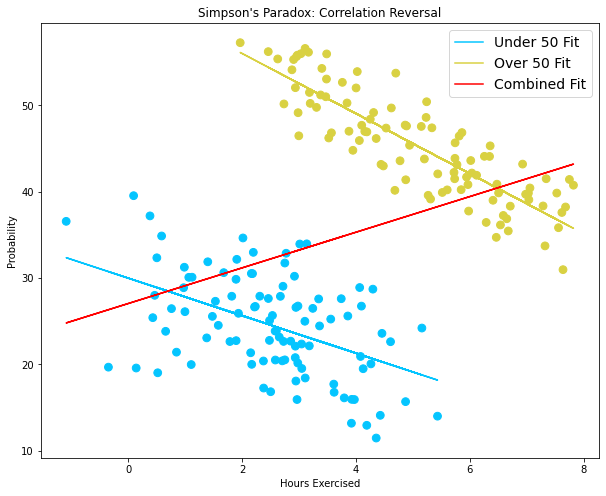
ここで散布図を使用してシンプソンのパラドックスについて読み解いてみましょう。
• 以下の図は運動時間(横軸)と病気の発生率(縦軸)の散布図です。
• 黄色が50歳以上、青が50歳未満のデータです。
• 今回はパラドックスが発生するように生成した疑似データであり、実データではないことに注意してください。(※3)
• 赤はデータ全体の相関を表しています。
この散布図を見て分かることは以下です。
1. 全体に対して運動時間と病気の発生率に弱い正の相関がある。
o運動するほど病気になる。
2. 50歳以上、50歳未満それぞれに対して運動時間と病気の発生率に弱い負の相関がある。
o運動するほど病気にならない。
データを全体で見た場合と年齢で分割した場合の帰結(相関係数)が逆転してしまいました。(シンプソンのパラドックス)
なぜこのようなことになったのでしょうか?
1. 年齢が高いほど病気の発症率が高くなる
という事実により、年齢が運動時間(横軸)と病気の発生率(縦軸)の交絡因子になっているということです。
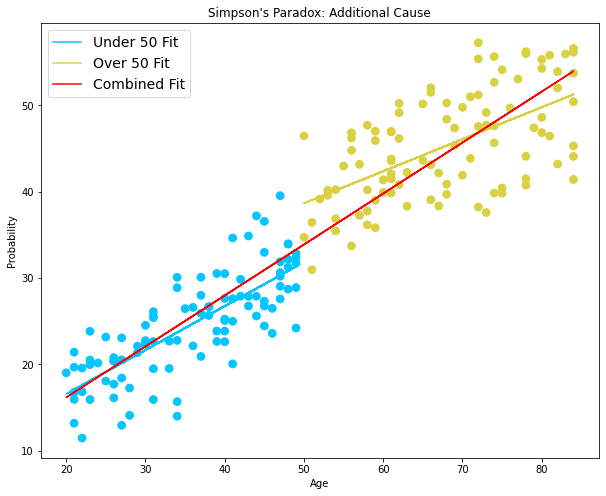
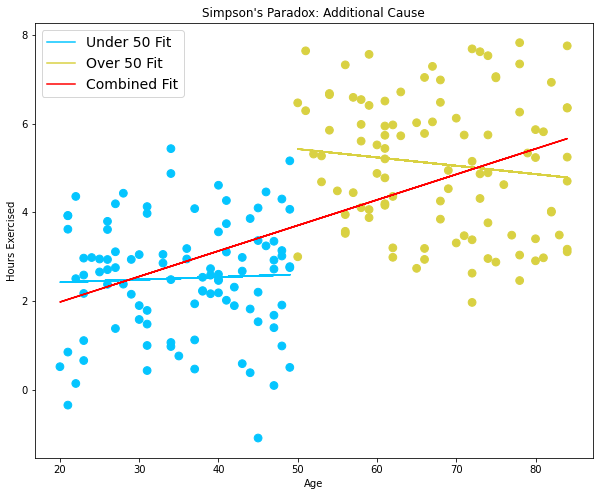
以下で、横軸を年齢にし、縦軸を病気の発生率と運動時間に変えたものをそれぞれ見てみましょう。
上記で記載した、年齢と病気の発生率の相関が見て取れますね。年齢と運動量も全体としては正の相関が見て取れますが、年齢別だと相関がほぼ無いようです。別の因子を特定しないといけないようです。
まとめ
今回はサンプルの生成データを使用して散布図を読み解きましたが、シンプソンのパラドックスに代表されるように、データに基づいて一見正しい主張をしているように見えてもデータを分割すると別の因子が見えてくることが多々あります。
上記を見てもわかる通り、統計データを読み解く上では、因子を特定する読み解き方、バイアスを適切に補正していくことが非常に重要なのです。
弊社ではこれまで多くの製造業、流通小売業をはじめ、通販/EC企業様のシステム構築支援を行っているのですが、それらの運用支援において、得られたデータの蓄積から経営判断を支援できるようなデータ分析も可能になっております。
また、2022年8月にタブレットお客様カルテ SHIORIというサービスを提供させていただいております。これは現在紙ベースの手書きで実施している業務をiPadを利用して電子化及びデータ化を支援するサービスです。たとえば、接客の際に作成する顧客カルテなどにおいて、データ化の手間を省力化し、そのデータを活用したVOC分析なども可能になります。今後、さらなるバージョンアップでデータ分析機能も強化していく予定です。
手書き業務の電子化やデータ分析などでお困りの場合はお気軽にご連絡ください。
※1 なるほど統計学園TOP
※2 バブルチャートの例として経済産業省が音頭を取っている化粧品産業ビジョンのレポートで利用されているものが非常にわかりやすかったです。
※3 今回のグラフ作成に当たってはData-Analysis/Simpson’s Paradox.ipynb at master · WillKoehrsen/Data-Analysis · GitHubを利用させていただきました。
記事 : Y.A